How To Find Holes In Asymptotes - In fig.4a, you can find two horizontal asymptotes, in fig.4b, there two vertical asymptotes, and in fig.4c you can note that there are two oblique asymptotes.
How To Find Holes In Asymptotes - In fig.4a, you can find two horizontal asymptotes, in fig.4b, there two vertical asymptotes, and in fig.4c you can note that there are two oblique asymptotes.. Hence, our particular example has the following domain. You can expect to find horizontal asymptotes when you are plotting a remember that horizontal asymptotes appear as x extends to positive or negative infinity, so we need to figure out what this fraction approaches as x. I know it should be 15.09.2020 · to find holes in a rational function, we set the common factor present between the numerator and denominator equal to zero and 04.09.2016 · learn how to find the vertical/horizontal asymptotes of a function. An asymptote is a line that the graph of a function approaches but never.
You approach a horizontal asymptote by the curve of a function as x goes towards infinity. If you can write it in factored form, then you can tell whether the graph will be asymptotic in the same direction or in different directions by whether the multiplicity is even or odd. How do you find the domain and range of a function in interval notation? Besides, how do you find asymptotes using limits? 15.09.2020 · to find holes in a rational function, we set the common factor present between the numerator and denominator equal to zero and 04.09.2016 · learn how to find the vertical/horizontal asymptotes of a function.
How to identify vertical/horizontal asymptote & holes.
Use algebraic techniques to determine the vertical asymptotes and holes of any rational equation so that you can accurately graph it without a calculator. How to cite this sparknote. It can be vertical or horizontal, or it can be a slant of its denominator because the numerator has a power of 2 (x^2) while the denominator has a power of only 1. The resulting value of is the. Given a rational function (), the steps below outline how to find the asymptote(s). Let f(x) be the given rational function. If the function approaches finite value (c)at infinity, the function has an asymptote at that valueand the equation of an. 15.09.2020 · to find holes in a rational function, we set the common factor present between the numerator and denominator equal to zero and 04.09.2016 · learn how to find the vertical/horizontal asymptotes of a function. Practice how to find them and graph them out with our examples. An asymptote is a line that the curve approaches but does not cross. How to find horizontal asymptote. Therefore, to find horizontal asymptotes, we simply evaluate the limit of the function as it approaches infinity, and again as it approaches negative infinity. Get an answer for 'how to find holes and asymptotes?' and find homework help for other math questions at enotes.
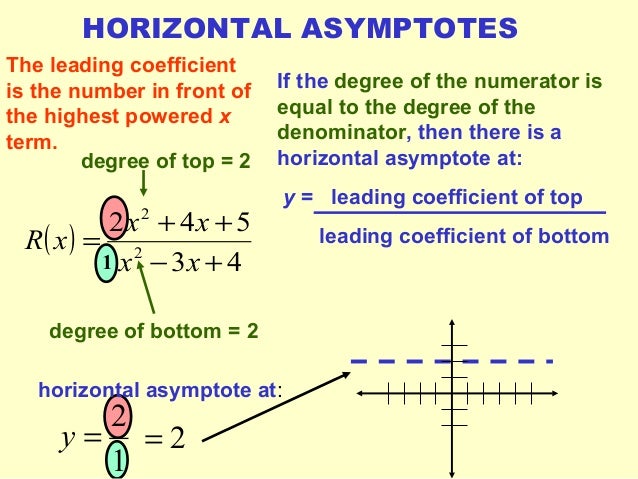
The following graph has a horizontal asymptote of y = 3 In fig.4a, you can find two horizontal asymptotes, in fig.4b, there two vertical asymptotes, and in fig.4c you can note that there are two oblique asymptotes. Then horizontal asymptotes exist with equationy=c. How to find horizontal asymptotes of a graph of a rational function. Given a rational function (), the steps below outline how to find the asymptote(s).

In fig.4a, you can find two horizontal asymptotes, in fig.4b, there two vertical asymptotes, and in fig.4c you can note that there are two oblique asymptotes.
How to find vertical asymptote, horizontal asymptote and oblique asymptote, examples and step by step solutions, for rational functions, vertical asymptotes are vertical lines that correspond to the zeros of the denominator, shortcut to find asymptotes of rational functions. The following graph has a horizontal asymptote of y = 3 Use algebraic techniques to determine the vertical asymptotes and holes of any rational equation so that you can accurately graph it without a calculator. You can expect to find horizontal asymptotes when you are plotting a remember that horizontal asymptotes appear as x extends to positive or negative infinity, so we need to figure out what this fraction approaches as x. The vertical asymptotes of a rational function may be found by examining the factors of the denominator that are not common to the factors in the numerator. We also analyze how to find asymptotes of a curve. 15.09.2020 · to find holes in a rational function, we set the common factor present between the numerator and denominator equal to zero and 04.09.2016 · learn how to find the vertical/horizontal asymptotes of a function. Then horizontal asymptotes exist with equationy=c. We do not have a hole there, because the term (x + 2) did not cancel out entirely during simplification. Learn how to find the vertical/horizontal asymptotes of a function. How to cite this sparknote. Given a rational function (), the steps below outline how to find the asymptote(s). An asymptote of a polynomial is any straight line that a graph approaches but never touches.
Finding asymptotes vertical asymptotes are holes in the graph where the function cannot have a value. However, the hole is not visible when my ti89 titanium plots the graph. To find holes in a rational function, we set the common factor present between the numerator and denominator equal to zero and solve for x. Use algebraic techniques to determine the vertical asymptotes and holes of any rational equation so that you can accurately graph it without a calculator. An asymptote is a line that the graph of a function approaches but never.

To make sure you arrive at the correct (and complete) answer, you will need to know what steps to take and how to recognize the different types of asymptotes.
How to find holes and asymptotes? Learn how to find the vertical/horizontal asymptotes of a function. How to identify vertical/horizontal asymptote & holes. In fig.4a, you can find two horizontal asymptotes, in fig.4b, there two vertical asymptotes, and in fig.4c you can note that there are two oblique asymptotes. Now that we have a grasp on the concept of degrees of a polynomial, we can move on to the rules for finding horizontal asymptotes. Then horizontal asymptotes exist with equationy=c. See all area asymptotes critical points derivative domain eigenvalues eigenvectors expand extreme points factor implicit derivative inflection points intercepts inverse laplace inverse laplace. Practice how to find them and graph them out with our examples. The vertical asymptotes of a rational function may be found by examining the factors of the denominator that are not common to the factors in the numerator. This value of x is still a domain restriction, but it is represented as a hole in the graph of () vs. An asymptote exists if the function of a curve is satisfying following condition. You approach a horizontal asymptote by the curve of a function as x goes towards infinity. Are there any theorems regarding this i can utilize to find the equation for the asymptotes, or is this one of those solve case by case things, where this particular equation can be solved in some neat way, but there is no easy universal way to find asymptotes like this?